海水中の音波減衰 --解説--
海水中を伝搬する音波は、音源からの距離が離れるにしたがって弱くなっていく。これは、海水中で伝搬損失を受けるためで、音源から拡散による減衰(拡散減衰 TL)と伝搬経路に存在する海水固有の吸収損失aを受けるためであり、伝搬損失は、これら2つの損失の和である。計算サイト
1.拡散損失

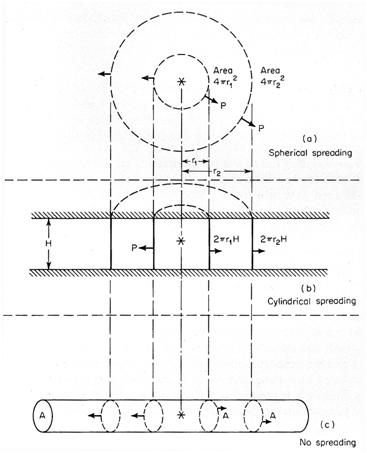
図1 海洋における音波の拡散(発散)モデル
図1(a)のように何も拘束のない音場(自由音場)では、音波は球面状に拡散していくため,音圧は、球の表面積(4pr2
r =
半径)のように広がり、すなわち距離の2乗で弱くなっていく。
海面と海底を境界として音波が反射して伝搬していくような場合(図1(b))は、海洋は大きな2次元的な伝搬路を形成するため、ある距離から円筒状に拡散していくこのときの音圧は、円柱の側面の面積(2πrh (r = 底面の半径、h = 高さ))、すなわち単純に距離とともに弱くなっていく。 さらに、実際の海洋では、起こりえないが、もし図1(c)のように円柱伝搬経路が形成されれば伝搬経路での面積が変化しないため拡散損失は生じない。
音源からの距離
r(m)としたときの球面拡散の拡散損失TLsと円筒拡散TLcは、各々以下のように表せる。
TLs=20log
r (dB)
TLc = 10log r (dB)
2.吸収損失
拡散損失のほかに、海水中を音波が伝搬していく過程で音響エネルギーが他のエネルギーに変換されることによって生じる減衰があり、これを吸収損失と呼ぶ。吸収のメカニズムは、水の粘性と熱伝導による古典的な作用と媒質中の分子による緩和作用があり、
熱的な緩和作用は、無視できるレベルであり、構造的な緩和作用としては、体積粘性の影響としてあらわれる。化学的な緩和作用は、海洋に含まれる少量の塩類により起こる吸収であり、ホウ酸と硫酸マグネシュウムの緩和作用がある。
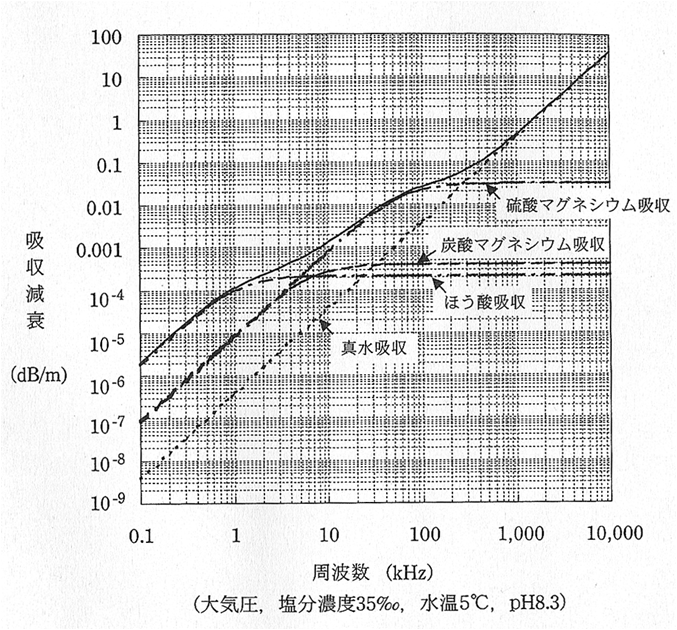
吸収の研究では,まず真水の吸収が発見され,その後,第二次世界大戦でのソーナーの研究に伴い硫酸マグネシウムによる吸収が発見された。戦後,より低周波の研究が進められ,ほう酸による吸収が発見された。
一般に,
海水中における音波の吸収(吸収損失)a
(単位はdB/km
--1kmあたりどの程度音が弱くなるかという意味--)は,様々な実測値を基に、いろいろな研究者によって実験式が作成されてきた。これらの実験式は、主に米国音響学会誌(Journal
of the Acoustical Society of America -J.A.S.A-)に発表されたもので、有名なものとして、Thorp(1961),
Schulkin & Marsh(1962)
,Fisher
& Simmon (1977) , Francois & Garrison(1982)及びAinslie
& McColm(1997)らの式がある。以下にそれぞれの実験式を説明する。
(1)Thorp
の式 1961年 (文献1)
Thorpの実験式では、aは、単純に周波数f(kHz)の関数として次式で表される。

しかし、Thorpの式では、周波数f以外の条件は、水温4℃、塩分35‰、PH 8、水深1000mと固定値であるため、それ以外の値では、当然誤差は大きくなる。一般にThorpでのaは、実際の値より大きめに出る傾向があるとされている。(文献2)
(2)Schulkin & Marshの式 1962年(文献3)
低周波まで拡張したSchulkin & Marsh の実験式は,周波数,塩分,温度,圧力,pH
及び音速の関数として次のように示される。
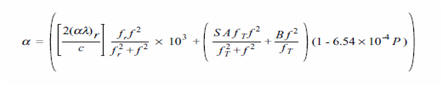
![]() ----
(2)
----
(2)
式(2)の各係数は次のように与えられる。
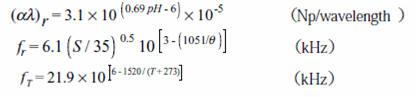
ここで,(al)
r
、は1波長当たりの最大吸収,fr
はほう酸の緩和周波数,A(= 2.34 ×10-6)は硫酸マグネシウムの緩和に関する定数,B(»
3.38
×10-6)は真水の粘性に関する定数,fT
は大気圧での温度依存の硫酸マグネシウムの緩和周波数,θ= 273 +T,T
は温度(℃),P は圧力(atm),c
は音速(m/s ),f は周波数(kHz),pH
は水素イオン濃度,S は塩分(‰)である。
(3)Fisher & Simmon( F&S )の式 1977年 (文献4)
Fisher-Simmonsの実験式は,周波数・温度及び圧力の関数として次のように表わされる。
この式では、吸収をホウ酸と硫酸マグネシュウムと真水による寄与による項として別々に求めている。式の第1項はほう酸の寄与,第2項は硫酸マグネシウムの寄与,第3項は真水の寄与を示している。

総吸収量 = ホウ酸の寄与+硫酸マグネシュウムの寄与 + 真水の寄与
 ---(3)
---(3)
ここで各係数は、
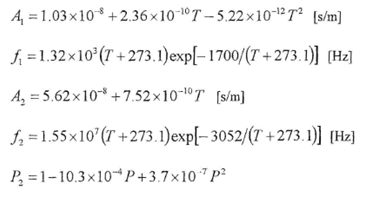
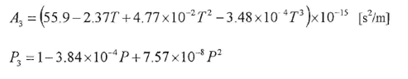
であり,f(Hz)は周波数,
T
(℃)は温度,
P
(atm)は圧力である。
(4)Francois
& Garrison ( F&G )の式 1982年 (文献5,文献6)
Francois & Garrisonの式
(6)は,周波数,pH
,塩分,温度及び深度の関数として次の式で示される。この式では、吸収をホウ酸と硫酸マグネシュウムと真水による寄与による項として別々に求めている。式の第1項はほう酸の寄与,第2項は硫酸マグネシウムの寄与,第3項は真水の寄与を示している。

総吸収量 = ホウ酸の寄与+硫酸マグネシュウムの寄与 + 真水の寄与
 ------(4)
------(4)
各係数は次のように与えられる。


ここで,f1,f2はほう酸と硫酸マグネシウムの緩和周波数,P1,P2,P3は圧力依存,A1,A2,A3は水の特性で変化する定数項である。A1,は海水のpH
により変化し、A2は塩分とともに増加し,A3
は温度が上がると減少する,f1 は温度と塩分で変化し,f2,
は温度とともに増加する。 q
=
273 + T,cは音速,pHは水素イオン濃度,fは周波数(kHz),Sは塩分(‰)-千分率-,T
は温度(℃),D は深度(m)である。
(4)Ainslie and McColm (A&M) 1997年 (文献7)
Ainslie and McColm (A&M)の実験式は、(3)のFrancois
& Garrisonのデータセットを基に作成され、最も新しい。A
& Mは、F
& Gよりも単純だがより実験値と良く合っていると主張している。

総減衰量 = ホウ酸の寄与 + 硫酸マグネシュウムの寄与 + 真水の寄与
 ----(5)
----(5)
A & Mでは、粘性による減衰aは、f, T と D の関数として以下のように表される。
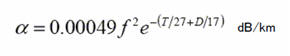
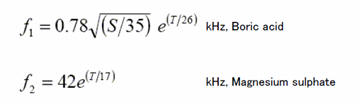
海水の性質を意味するのに用いられる他のパラメータは、酸性度またはpHである。F & Gにおいては、典型的海洋の値(ライマンとフレミングの提案値)は、pH = 8であり、すべての海は、pHでいくぶんアルカリ性であることを示している。しかし、近年、これが地球温暖化と関連して大気中の二酸化炭素の吸収によって酸性に変わっており、これにより伝搬減衰が小さくなるという問題が提起されている。文献(8)
緩和メカニズムのための吸収には、以下のような特徴のある型がある。
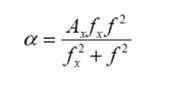
ここでAx
は、定数でfxは、緩和周波数である。
A&Mにおいては、総減衰量を求めるために、比較的単純な表現を2つの化学緩和作用関連した定数Axとして与える。

A&Mでは、従来は、酸性度が低周波におけるホウ酸吸収に影響を及ぼすだけだったのに対して、塩分が中間の周波数の吸収を起こし、低周波吸収を減少させる点に注目している。そして、水温は、2つの緩和周波数付近以外の吸収を減少させる。
以下のグラフは、横軸に周波数(kHz)、縦軸にA&M(1998)により求められた周波数と真水の寄与、ホウ酸の寄与硫酸マグネシュウムの寄与及び総減衰量(dB/km)を表している。

また、以下にはそれぞれ異なる海洋(太平洋、紅海、北極海、バルチック海)における減衰を求めている。
